Apr 28, · 第一:直角三角形边长公式:c²=a²b² :已知三角形两条直角边的长度 ,可按公式c²=a²b²计算斜边。 2/4 第二:直角三角形边长关系: 1、两边之和大于第三边;2、直角三角形中两直角边的平方和等于斜边的平方 (c²=a²b²)。 3/4三角形の重心 このテキストを読み始める前に、三角形の重心の性質についてよくわからないという人は、こちらのテキストを読んでおきましょう。 ・agを延長してbcと交わる点m₁は、bcの中点にあたる。 そしてag:gm₁=2:1 ・bgを延長し你好 平面图形没有体积 同理就不存在表面积了 面积公式: 长方形=长x宽 正方形=边长x边长 三角形=底x高÷2 梯形=(上底下底)x高÷2
正三角形 维基百科 自由的百科全书
正 三角形 の 公式
正 三角形 の 公式-Feb 19, 21 · この記事では、「正三角形」の定義や面積の公式を解説していきます。 また、高さ・角度・重心・辺の長さの求め方についても紹介していくので、ぜひマスターしてくださいね! 目次正三角形とは?定義正三角形の定理(性質)正三Sep 03, · 三角形の角度の合計は180度です 🔊 Play The angles of an equilateral triangle are all 60 degrees 正三角形の角度は、すべて60度です 🔊 Play The area of triangles is half of the base times the height 三角形の面積は、底辺×高さ÷2です 四角形 quadrangle, quadrilateral




正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean
三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていきDec 26, 19 · 正三角形面积公式为:S= (√3)a²/4,(S是三角形的面积,a是三角形的边长) 1、三角形面积公式为:S= (1/2)ah (S是三角形的面积,a是三角形的一条边,h是这条边上的高) 2、正三角形,三条边相等,三条边上的高也对应相等,边长为a,高为h,则h= (√3)a/2 所以Jun 27, 18 · 截面三角形惯性矩的公式推导 26;
指定された正三角形の高さから公式で1辺の長さ,面積を計算し表示します。 1辺の長さaが1の正三角形 高さ h: 面積 S:1307 三角形,矩形,圆形的惯性矩公式怎么导出的? 各种截面的惯性矩怎么计算? 17;正三角形的中心 : 当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心三角形只有五种心 重心三条中线的交点,三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍;重心分中线比为12(也称中心);垂心三角形三条高的交点;
一般角 θ に対する、 三角関数(sin, cos, tan)の定義 は次の通りです。 座標平面上に、原点 O O を中心とする半径 r r の円を描く。 x x 軸の正の部分を始線として、角 θ θ の動径と円 O O との交点の座標を P(x,y) P (x, y) としたとき、 sinθ,cosθ,tanθ sinDec 10, 18 · 解直角三角形(斜三角形特殊情况): 勾股定理,只适用于直角三角形(外国叫"毕达哥拉斯定理") a^2b^2=c^2, 其中a和b分别为直角三角形两直角边,c为斜边。正三角形の面積 1辺の長さから正三角形の面積,以下のように三角形の3辺の長さを代入することで面積を計算する公式です。 5/6/19 · 正三角形の高さと面積を求める公式について説明します。 作者 數學部屋 ・正三角形の面積計算 1辺の長さaの正三角形の




中学2年生 正三角形の定義と性質 公式 個別進学教室マナラボ受験 教育情報サイト




小5 面積 三角形の面積の求め方 日本語版 Youtube
三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)Jun 02, 21 · 正三角形面积公式 S=1/2a²sin60°=1/2ah=√3/4·a² 正三角形的性质: 具有等腰三角形的所有性质,结合定义更特殊 1、等边三角形的内角都相等,且为60度 2、等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)第一题纯粹就是算术,送分题,这里作者就不讲解了 第二题: 标题:纸牌三角形a,2,3,4,5,6,7,8,9 共9张纸牌排成一个正三角形(a按1计算)。 要求每个边的和相等。 下图就是一种排法(如有对齐问题,参看p1png)。 a 9 64 7 5 2这样的排法可能会有很多。




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




直角三角形 Wikipedia
正余弦转换公式 诱导公式(口诀奇变偶不变,符号看象限。 两角和与差的三角函数公式 万能公式 sin(α +β )=sinα cosβ +cosα sinβ sin(α -β )=sinα cosβ -cosα sinβ cos(α +β )=cosα cosβ -sinα sinβ cos(α -β )=cosα cosβ +sinα sinβ tan(α +β( 点击多边形工具 在属性栏上多边形端点数设置为3 然后按住CTRL键就可以画很标准的三角形了 ) 如何用尺规作圆内接正三角形?May 31, 21 · まず正五角形は三角形3つの集まりで表せるので、内角の和は180×3で540°。 内角は5つなので540÷5=108(°)となる。 正五角形の内角は108° するとここを頂角にした二等辺三角形が見えてきたと思うので、底角を出す。さっそく二等辺三角形が出てきてうれしい。
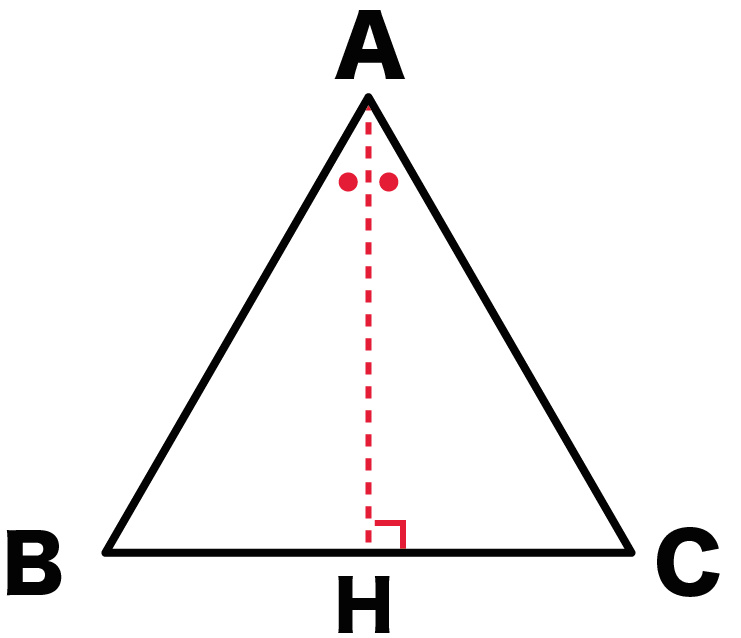



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3
正三角形の面積,正四面体の体積 正三角形の面積はもちろん,正四面体の体積も一瞬で求められるようにしておきましょう。 サラスの公式 座標平面,座標空間上での求積はサラスが強力。 ベクトルの定番問題の公式(面積比) 超頻出です。Oct 02, · 正多边形 内角计算公式与半径无关 要已知 正多边形 边数为N 内角和=180 (N2) 半径为R 圆的内接三角形面积公式 (3倍根号3)除以4再乘以R方 外切三角形面积公式3倍根号3 R方 外切正方形4R方 内接正方形2R方 五边形以上的就分割成等边三角形再算 内角和公式簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ For more information and source, see on this link https//jukenmikatanet/howto/mathematics/equilateraltriangleareaformulahtml



正三角形の個数




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
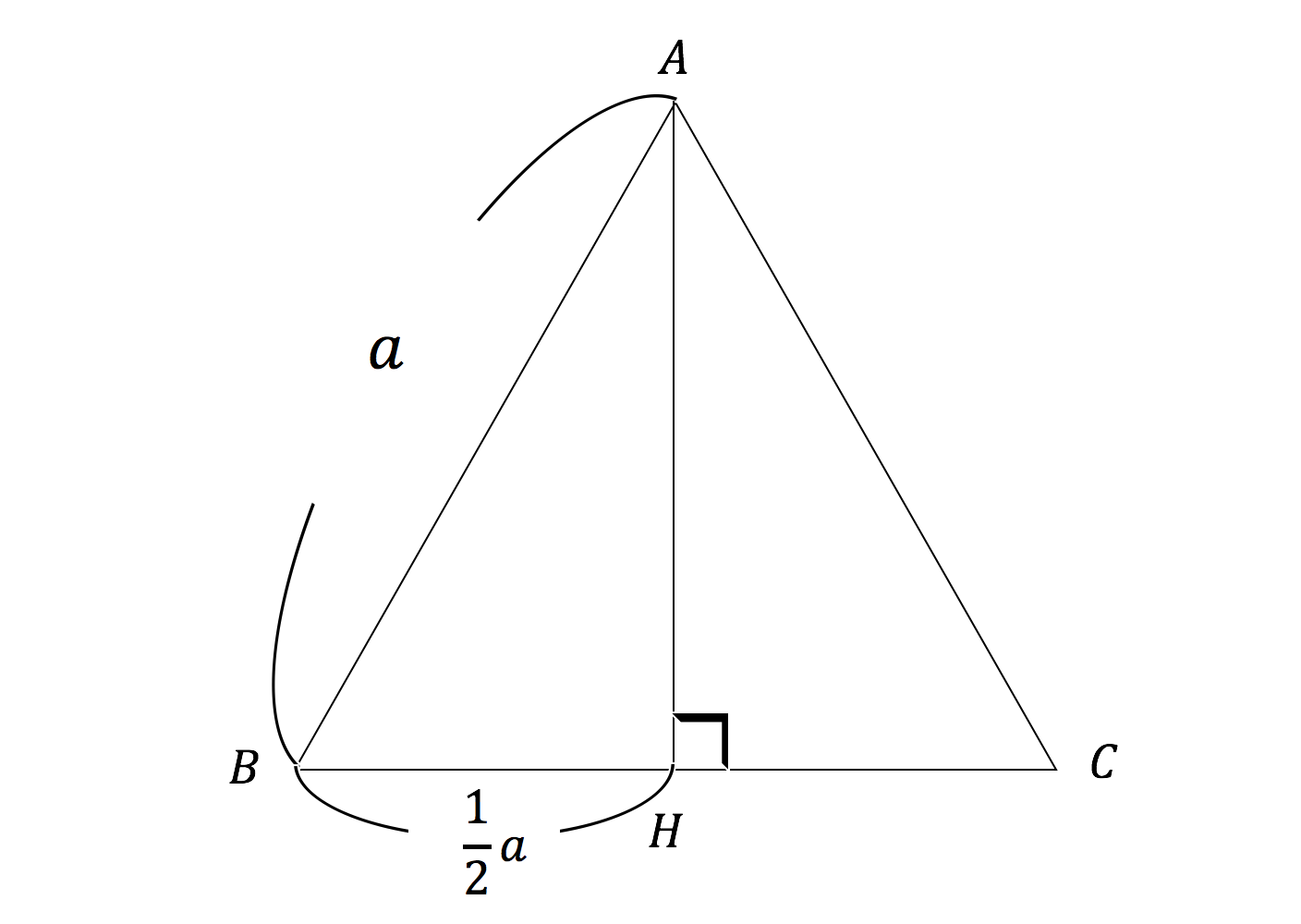
正三角形の特徴、特性、公式および面積 A 正三角形 それは3辺を持つ多角形です。 つまり、それらは同じ基準を持っています。 その特性のためにそれは正三角形の(等辺)の名前を与えられました 三角形は、3つの側面、3つの角度、3つの頂点で形成されMar 06, 21 · V=\dfrac {\sqrt {2}} {12}a^3 V = 122 a3 記述式の場合途中経過を求められるので,この公式を用いることはできませんが,検算に用いることはできます。 特に, (ii)はその場で計算しようとするとわりと時間がかかってしまうので,覚えておくべきです。 正四面体の体積は「底面積×高さ× 1 3 \dfrac {1} {3} 31正三角形 提出时间 约17世纪 应用学科 数学,几何 边长公式 C=3a 面积公式 S=(√3)/4*a^2
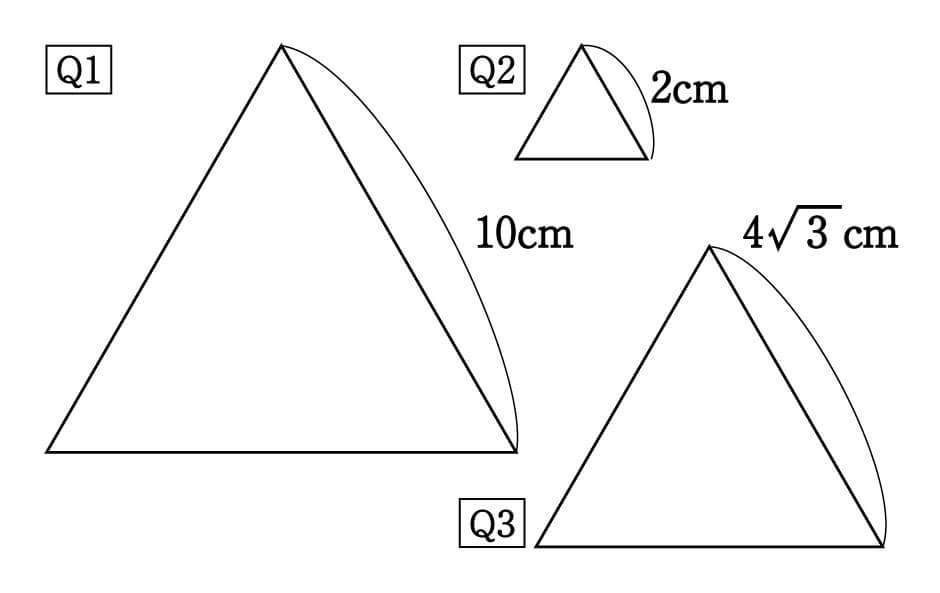



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
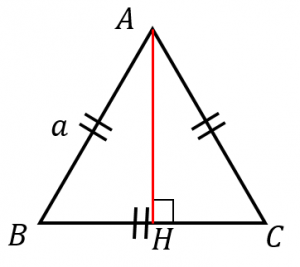



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学
May 30, · 当我们知道等边三角形的边长后,我们还可以采取另外一种方法来计算等边三角形的高。 h=l*sin60° 6/6 或者可以通过公式:h=l*cos30° 计算 编辑于0530,内容仅供参考并受版权保护 赞 踩 分享Sep 12, 10 · 6 、三角形任意两边之和大于第三边,任意两边之差小于第三边。 7、 在一个直角三角形中,若一个角等于30度,则30度角所对的直角边是斜边的一半。 8、直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。其三個內角相等,均為60°。它是銳角三角形的一種。設其邊長是 ,則其面積公式為 。 等邊三角形是正四面體、正八面體和正二十面體這三個正多面體面的形狀。六個邊長相同的等邊三角形可以拼成一個正六邊形。




簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




三平方06 正三角形の面積 Youtube
用相同的正多边形镶嵌:只用一种多边形时,可以进行镶嵌的是三角形、四边形或正六边形。 用不同的正多边形镶嵌: (1)用正三角形和正六边形能够进行平面镶嵌; (2)用正十二边形、正六边形,正方形能够进行平面镶嵌。 平面图形常见公式:Jun 28, 21 · 正方形的对角线,与两边成形的是等腰直角三角形。如果正方形的边长为a,那么对角线的长度就可以根据勾股定理计算,对角线=√2a。 对角线公式 正方形对角线长度即边长乘以2的平方根,或2a²的平方根V=a√2 v为正方形的对角线,a为正方形的边长。正多角形の面積公式一覧と導出方法を解説正二十四角形まで 21年1月28日 1辺の長さaの正方形の面積は、もちろん a 2 ですが、正三角形の面積公式は知っていますか 中学や高校の試験で登場するため、正三角形の面積公式は覚えておいて損はありませ
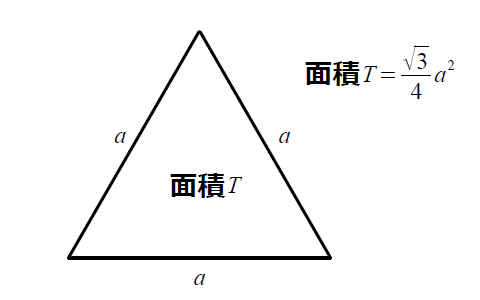



正三角形の面積計算 ゆるゆるプログラミング
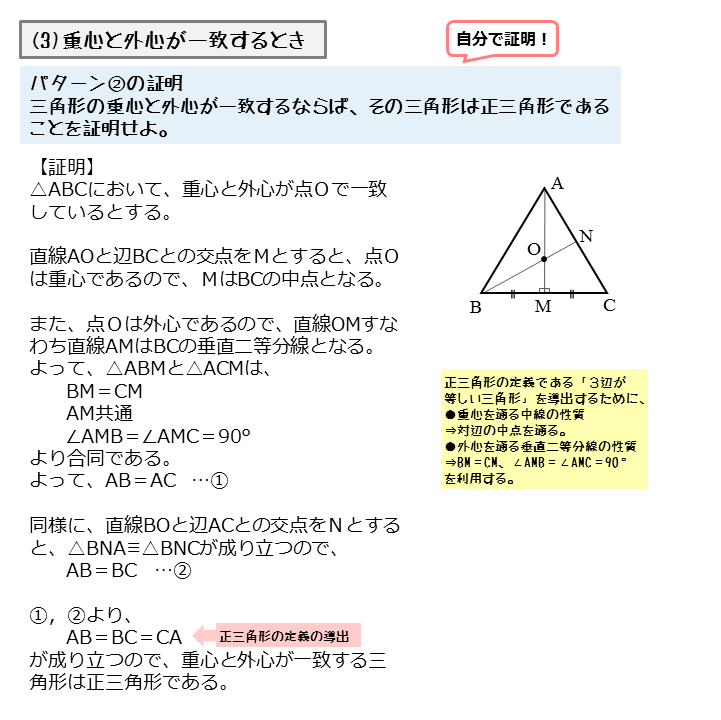



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
8 、 在 平面直角坐标系 内,A(a,b),B(c,d),C(e,f)构成之三角形面积为 。 A,B,C三点最好按逆时针顺序从右上角开始取,因为这样取得出的结果一般都为正值,如果不按这个规则取,可能会得到负值,但只要取绝对值就可以了,不会影响三角形面积的大小。 9、 ( 正三角形 面积公式,a是三角形的边长) 10、 (其中,R是 外接圆 半径;r是 内切圆 半径) 11三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。计算公式是: 面积 = w × h w = 宽 A 部份是个正方形: A 的面积 = a 2 = 米 × 米 = 400平方米 B 部份是三角形。横看它的底是 米而高是 14米。



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
A = 3 4 a 2 {\displaystyle A= {\frac {\sqrt {3}} {4}}a^ {2}} 外接圓 的半徑 R = 3 3 a {\displaystyle R= {\frac {\sqrt {3}} {3}}a} 內切圓 的半徑 r = 3 6 a {\displaystyle r= {\frac {\sqrt {3}} {6}}a} 以上公式可由 勾股弦定理 推導而得。 正三角形的垂足和其底邊的中點共點,因此正三角形的高也是其底邊的 中垂線 及 中線 ,高也會將頂點所的在的角平分。



1



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



2 59 第4章 二等辺三角形 正三角形の計算問題 Kakera Link 公式ブログ
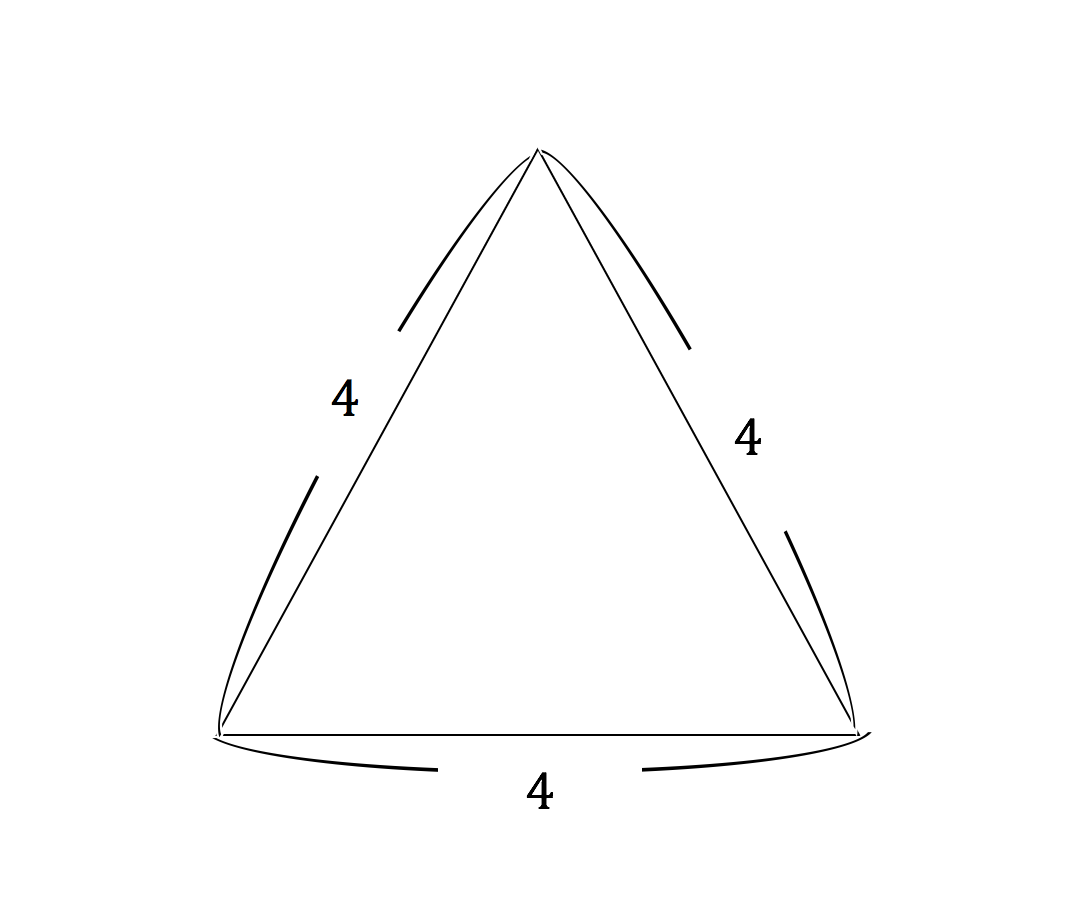



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典
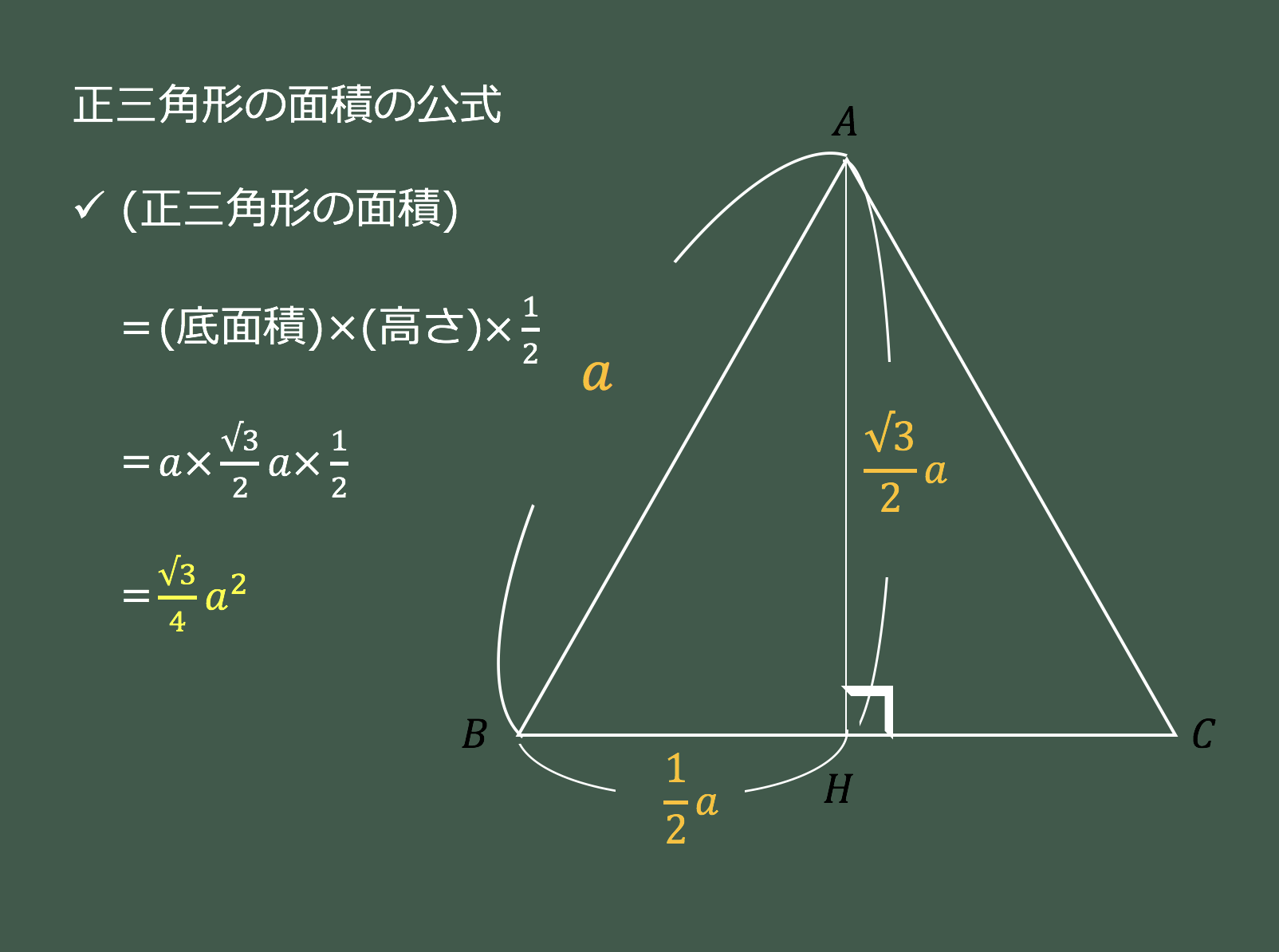



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



正三角形の高さの求め方は 1分でわかる計算 面積の求め方 二等辺三角形の高さの求め方
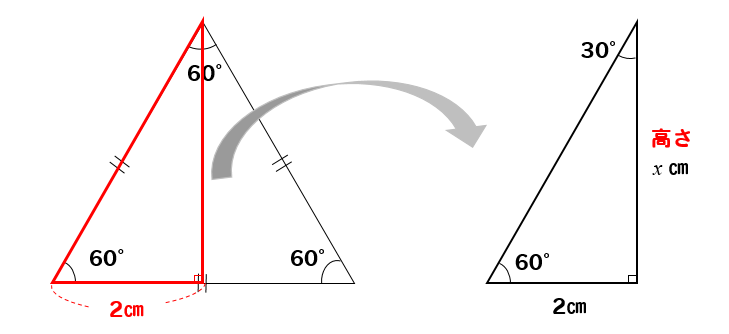



三平方の定理 正三角形の高さ 面積を求める方法を解説 数スタ
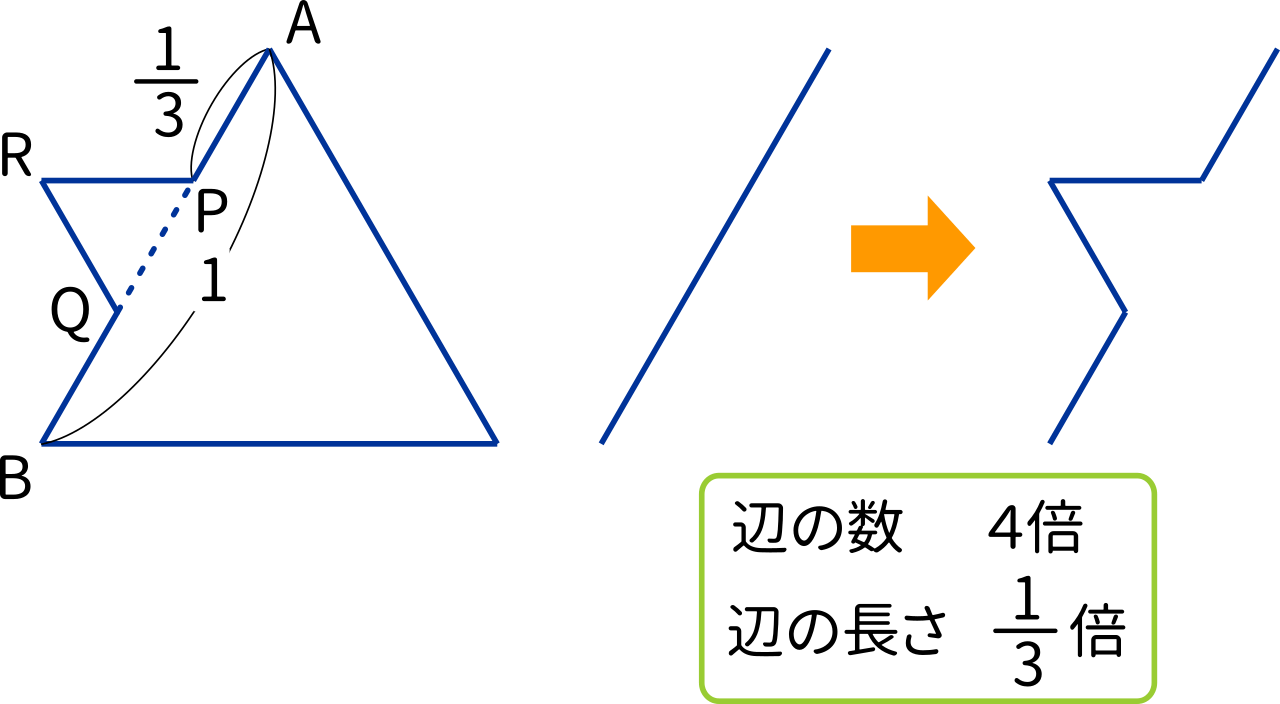



数 極限 図形と数列の極限 三角形が無限増殖するフラクタル 北海道大10後期 Mm参考書




正 三角形 面積




3 3 17 正三角形的高與面積 Youtube




最高 50 正三角形 面積 求め方
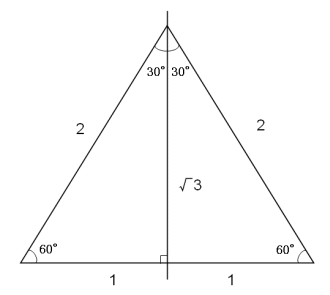



初等幾何 正三角形がつくる直角三角形 大人が学び直す数学
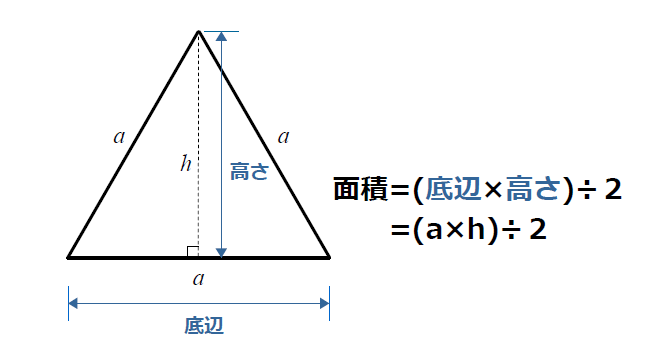



正三角形の面積計算 ゆるゆるプログラミング



正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




正三角形的高與面積計算 Math Height And Area Of An Equilateral Triangle Youtube



3




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月




正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean
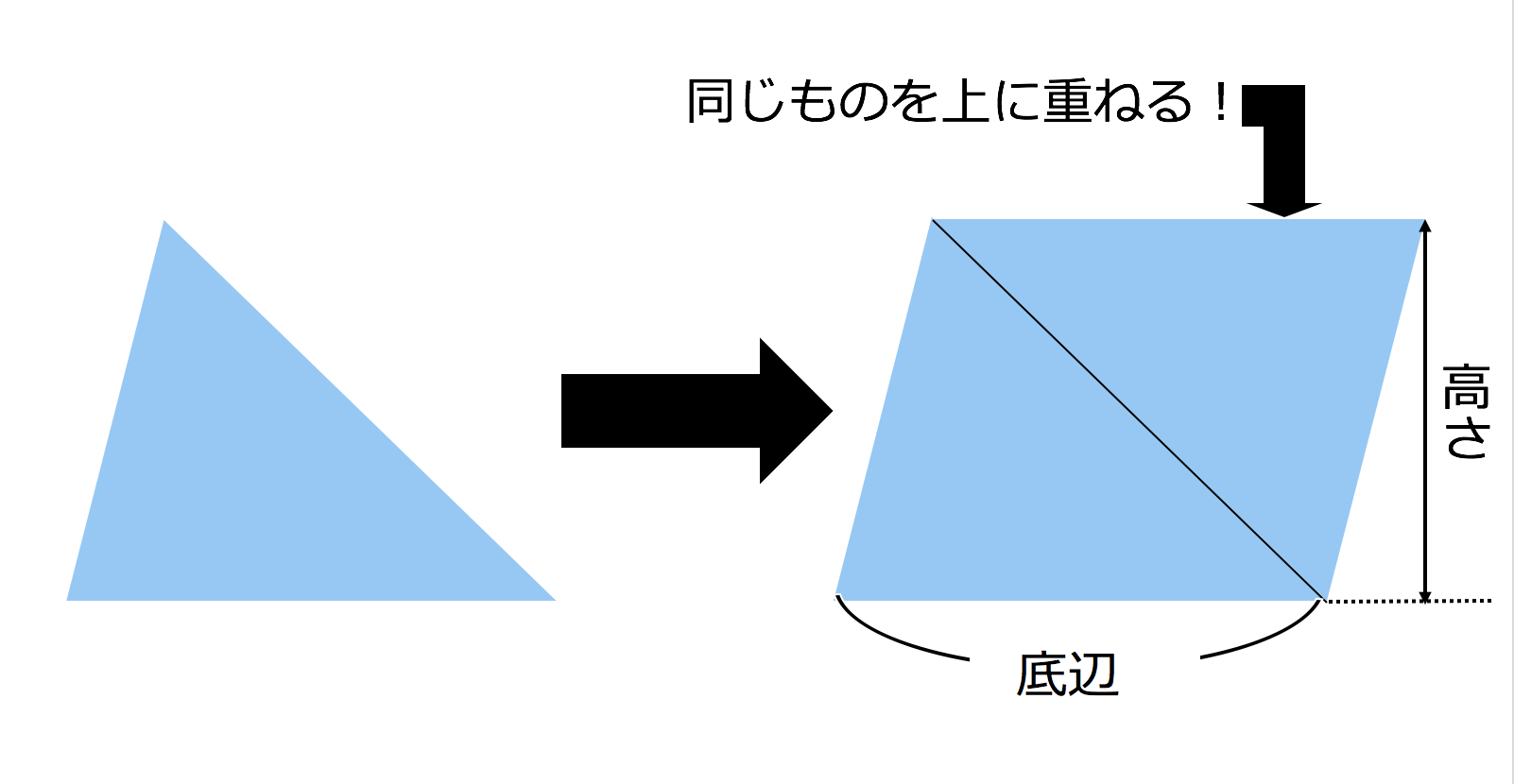



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




三角形の面積を求める公式まとめ 高校数学の美しい物語




3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ
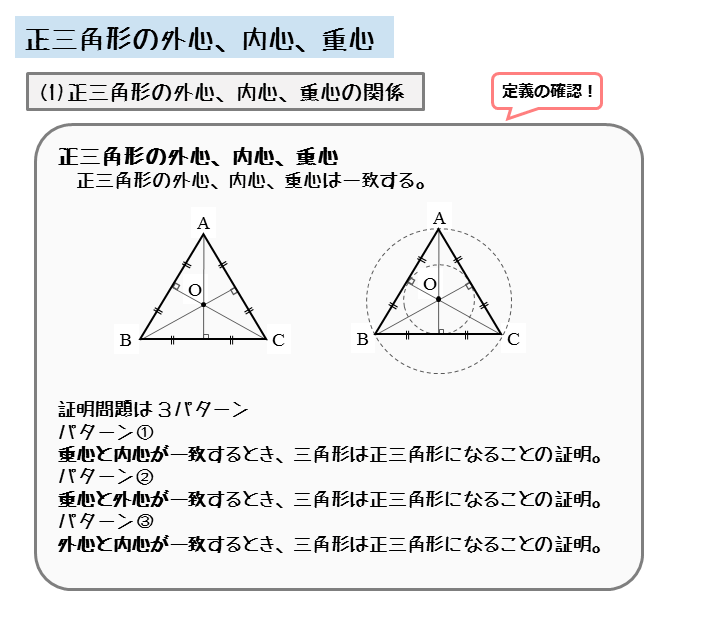



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
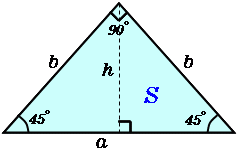



直角二等辺三角形 高精度計算サイト



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



雑学のソムリエ 正三角形の面積



一辺が9センチの正三角形の高さをもとめてください式もおねがいします 三平 Yahoo 知恵袋



正三角形 维基百科 自由的百科全书




翻轉學習影片 國中 數學 三角形基本性質 正三角形




正多面体の種類と性質 面 辺 頂点の数の公式 数学fun




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
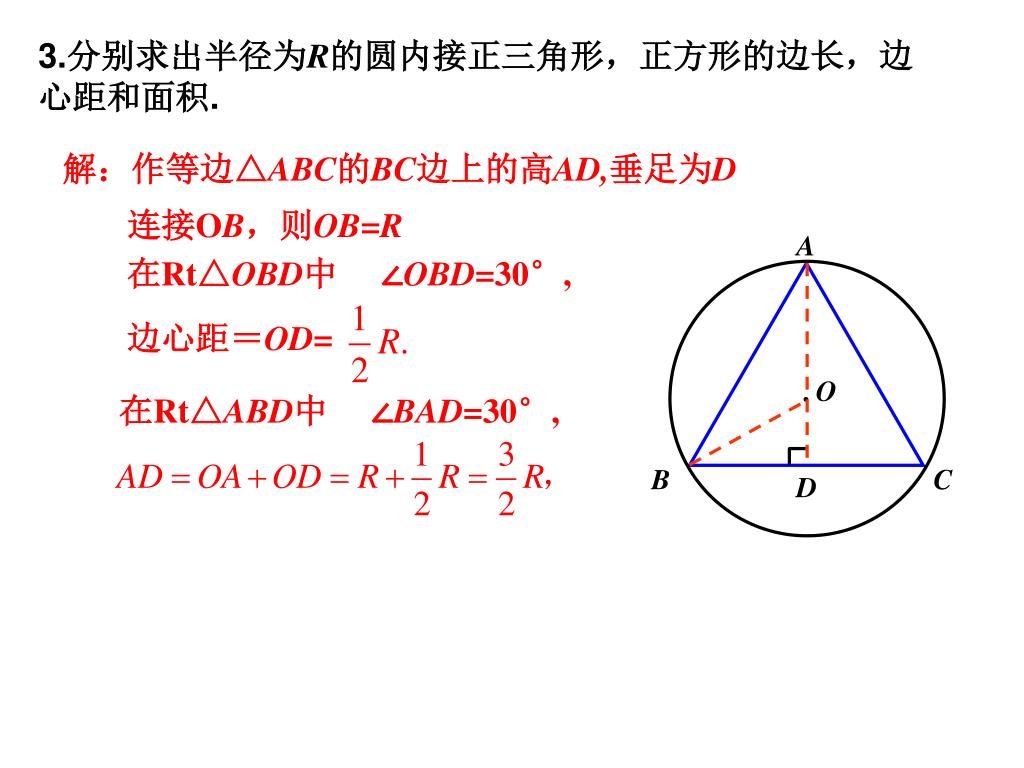



正 三角形 面積
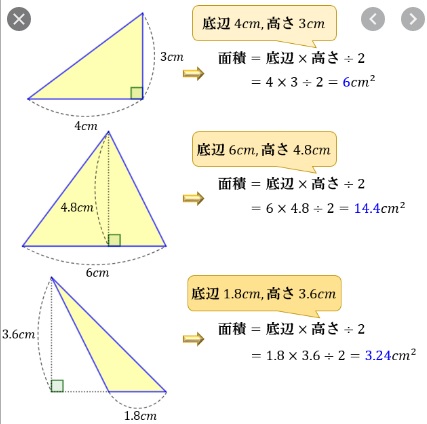



三角形の面積 中学受験 塾なし の勉強法




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




サイン Sin を使った三角形の面積を求める公式とその証明 数学i By ふぇるまー マナペディア
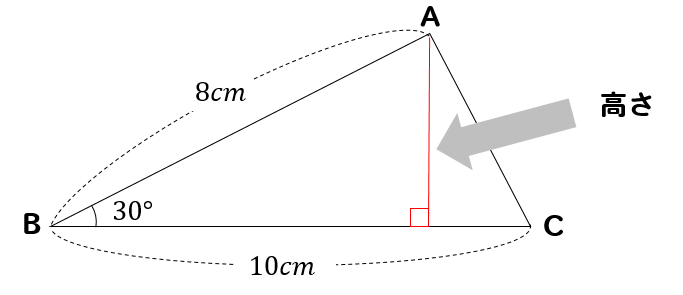



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




例題 正三角形的高與面積 畢氏定理 均一教育平台



Math 正三角形 正六角形と面積 同じ形に分けて考える問題 働きアリ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
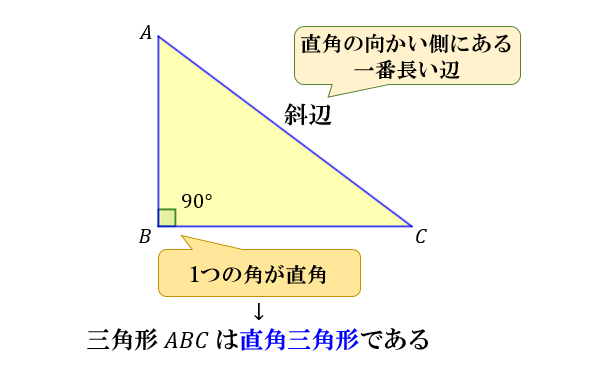



直角三角形の辺の長さ 合同条件 面積について アタリマエ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
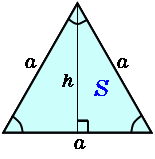



正三角形 高精度計算サイト
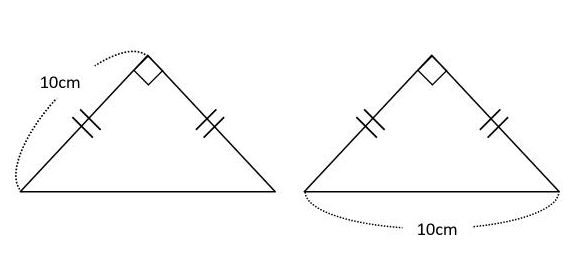



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
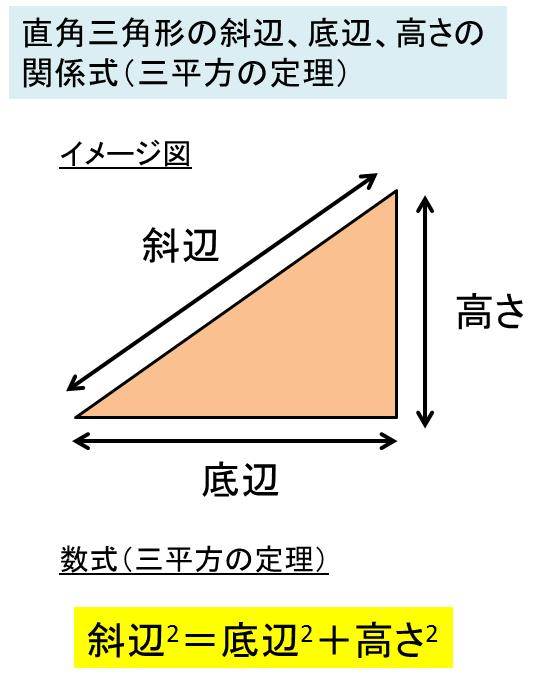



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




面積の求め方 計算公式一覧
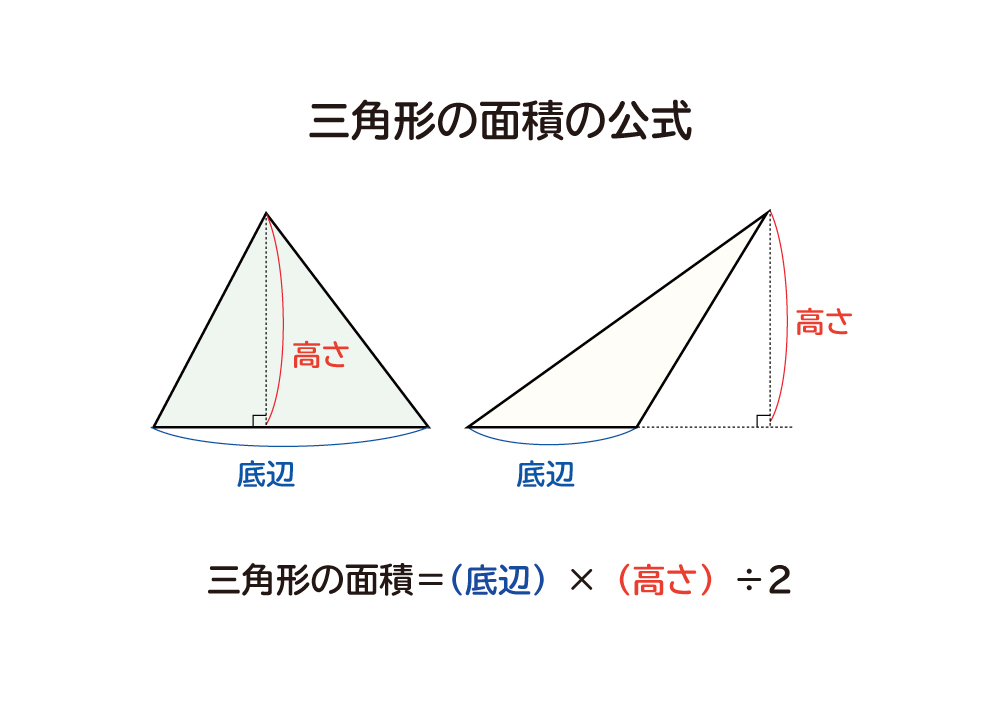



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
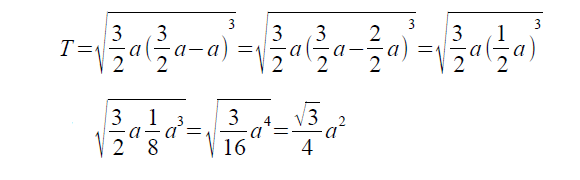



正三角形の面積計算 その2 ゆるゆるプログラミング




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




正三角形的高與面積計算 Math Height And Area Of An Equilateral Triangle Youtube




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学




正三角形を2等分する最短の境界線を求めよ 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
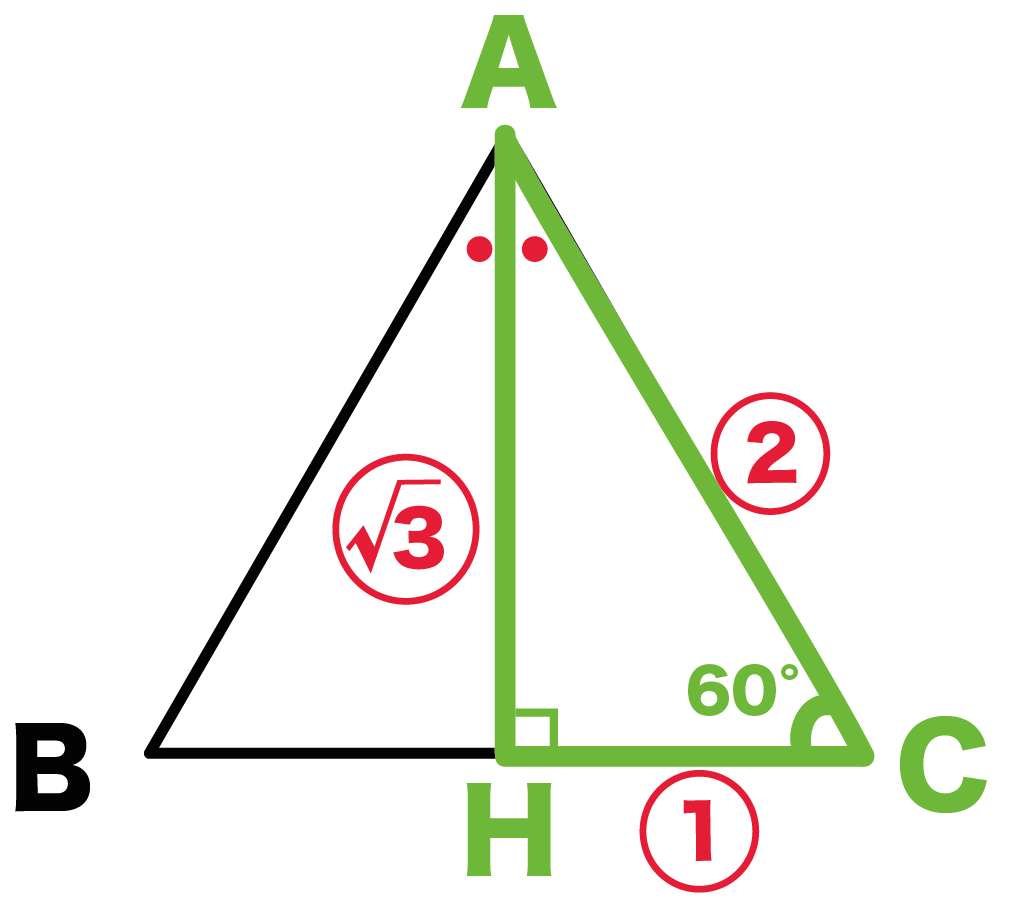



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
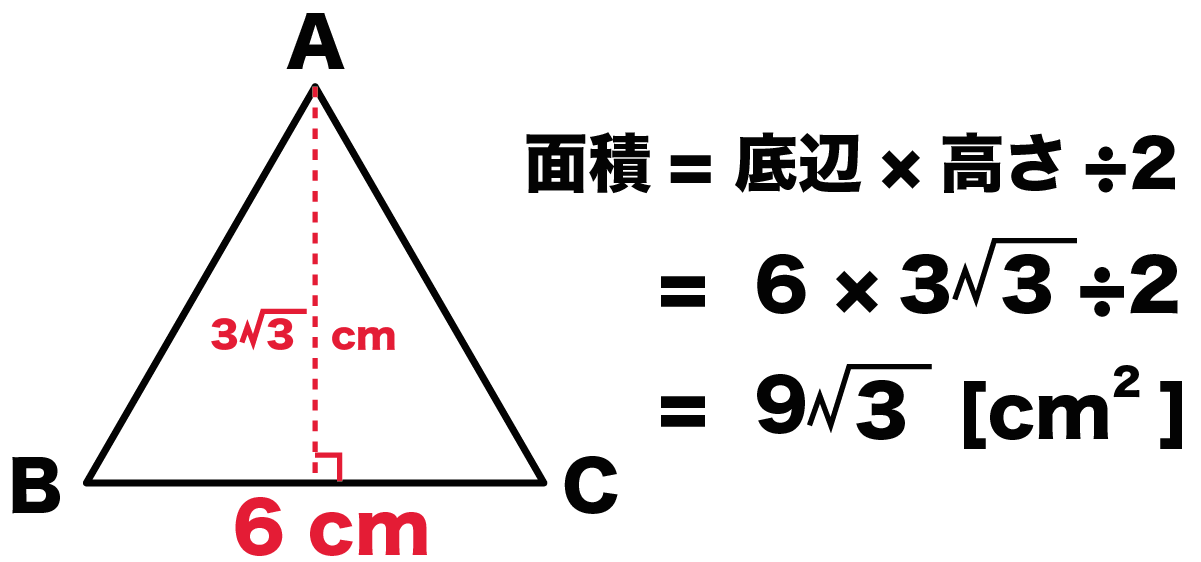



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ
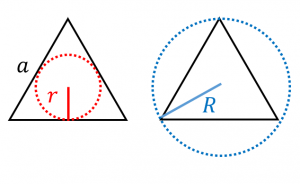



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学
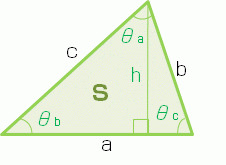



三角形の公式 Wakatta



小学3年生の算数 三角形 正三角形や二等辺三角形 練習問題プリント ちびむすドリル 小学生




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




正三角形の高さを求める3つの方法と求め方がわかる3ステップ 言葉 雑学 歴史を知るならmayonez



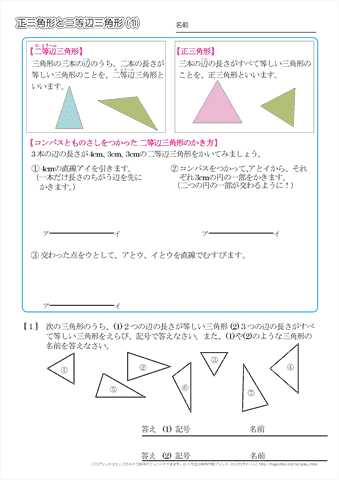
3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ




直角三角形の合同条件とその証明 数学fun




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




作図 円に内接する正三角形の作図方法とは 数スタ



1



最大の正三角形
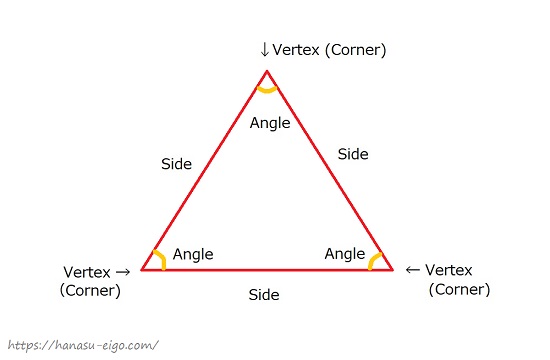



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




三角形の断面二次モーメントの求め方 平行軸の定理を使います おりびのブログ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




アスクル アムス 三角のファブリックパネル 正三角形30cm 1セット 10枚 直送品 通販 Askul 公式




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



三角形の面積と公式 面積計算機
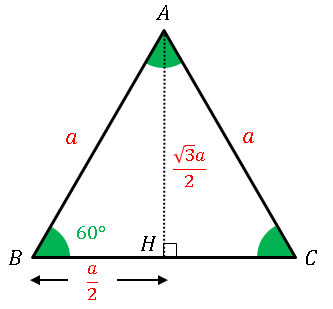



正三角形の性質 角度 面積 周の長さ 対称性




正三角形 Wikipedia




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
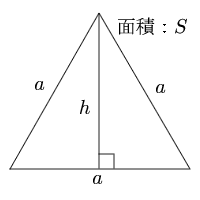



正三角形 面積の計算 計算サイト
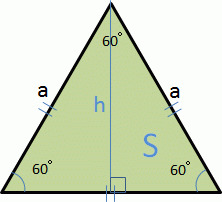



三角形の公式 Wakatta


